Today in Math class, we first corrected our homework from yesterday.
To join the perfect square club, you must be a full NUMBER, no decimals. EG: 4x4
If you do not belong to the perfect square club, you are imperfect. You are not a
PERFECT sideline number, you are not a full number. You have a demical. EG: 4.5x4.5

After we corrected out homework, Harbeck drew us 4 squares.
Just like this picture v. He then told us to describe it and write down 3 things about each square.


The first square has an area of 1. It is an all perfect square because one is one square unit. The sidelines are 1, and you get this by square rooting the area (1). so, squareroot1 = 1. So, 1x1, and 1 squared. This square is also the smallest square out of all of them, and it also belongs in the perfect square club because the sideline numbers are perfect numbers and don't have decimals.

This second square has an area of 2. It is NOT a perfect square because the square root of 2 is 1.414, which is obviously not a perfect number. So, the square cannot have a perfect sideline either. Squareroot2 = 1.414, 1.414x1.414 and 1.414 squared. This square is between the first and last square. This square would not be able to get into the perfect square club because the sidelines have decimals in them.

The third square has an area of 3. It is NOT a perfect square, because the square root of 3 is 1.732, which again is obviously not a perfect number. so the square cannot have a perfect sideline either. Squareroot3 = 1.732, 1.732x1.732, 1.732 squared. This square is between the first and last square. This square would not be able to get into the perfect square club because the sidelines have decimals in them.
The last square has an area of 4. It is a perfect square because the square root of 4 is 2 which is a perfect number. Squareroot4 = 2, 2x2, 2 squared. This is also the largest square in the whole picture, and it also belongs in the perfect square club because the sideline number is a full number with no decimals.
And lastly, he gave us homework.
HOMEWORK:
Make 9 squares and write down 3 things about them, and explain how they all fit together.
Heres what I think the answers are. (Sorry, It would take too long to draw 30 squares on paint.)
Square 5 - The square has an area of 5. It is not a perfect square because the square root of 5 is 2.236, which is obviously not a perfect number. This square would not belong in the perfect square club because the sideline numbers are not full numbers. (decimals). Squareroot5 = 2.236, 2.236x2.236, 2.235 squared. You can also find the perimeter by adding all the sideline numbers together. 2.236+2.236+2.236+2.236=8.944.
Square 6 - This square has an area of 6. It is not a perfect square once again, because the squareroot of 6 is 2.448, which is obviously not a perfect number. This square would not belong in the perfect square club because the sideline numbers are not full numbers once again. Squareroot6 = 2.448, 2.448x2.448 and 2.448 squared. You can also find the perimeter by adding all the sideline numbers together. 2.448+2.448+2.448+2.448=9.792.
Square 7 - This square has an area of 7. It is not a perfect square because the square root of 7 is 2.645, which is obviously not a perfect number. This square would not belong in the perfect square club because the sideline numbers are not full numbers once again. Squareroot7 = 2.645. 2.645x2.645, and 2.645 squared. You can also find the perimeter of the square by adding all the sidelines of the numbers together. 2.645+2.645+2.645+2.645=10.58
Square 8 - This square has an area of 8. It is not a perfect square because the square root of 8 is 2.828, which is obviously once again not a perfect number. This square would NOT belong in the perfect square club because the sideline numbers are not full numbers. Squareroot8 = 2.828, 2.828x2.828, and 2.828 squared. You can also find the perimeter by adding all the sideline numbers together. 2.828+2.828+2.828+2.828=11.312.
Square 9 - This square has an area of 9. It is a perfect square because the square root of 9 is 3, which is obviously a perfect number. This square would definitely belong in the perfect square club because the sideline numbers are full numbers. Square root 9 = 3, 3x3 and 3 squared. You can also find the perimeter by adding all the sideline numbers together. 3+3+3+3=12.
WELL, there. I don't really understand the last part of the homework, so I'll wait until tomorrow and see. I thought we had to talk about 30 squares! and I did 27, but then that time I checked my books and asked many people. And they all said 9. So, booo me. Anyways, thanks for reading! PLEASE comment. NEXT SCRIBE, I CHOOOOSE..... DEAN.
 Question: Which neighborhood is getting more hardtop than the other? (is there more hardtop in one lot than the other?
Question: Which neighborhood is getting more hardtop than the other? (is there more hardtop in one lot than the other?  Question: Which neighborhood is getting more hardtop than the other? (is there more hardtop in one lot than the other?
Question: Which neighborhood is getting more hardtop than the other? (is there more hardtop in one lot than the other? 
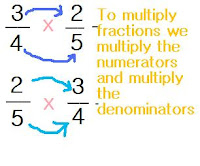
 I'm sorry. I'm BAD at math, so I got the above answer all wrong! The correction is: You start off with a square that's divided into four, and 3 fourths of it is shaded in. Then, you find out the common denominator! So since the denominator is 20, you divide the square into 20. Since it's now divided, into 5 lines, you shade in 2 parts of it from the 3 fourths that was shaded in. I know this doesn't make sense, I didn't get it either :(
I'm sorry. I'm BAD at math, so I got the above answer all wrong! The correction is: You start off with a square that's divided into four, and 3 fourths of it is shaded in. Then, you find out the common denominator! So since the denominator is 20, you divide the square into 20. Since it's now divided, into 5 lines, you shade in 2 parts of it from the 3 fourths that was shaded in. I know this doesn't make sense, I didn't get it either :( Since this is Flatbush, we divide this one into fifths first, then divide it by 4, into 20. 3 fourths of it is a simplified version of 6/20.
Since this is Flatbush, we divide this one into fifths first, then divide it by 4, into 20. 3 fourths of it is a simplified version of 6/20.