HARBECK, ILL MISS YOU
GAAP's (Maeddah's) 2 Minutes To Make A Difference
This is the video made by Gelli, Hanbit, Tracy and Maeddah. It is talking about Canadian Poverty and how it affects many people all around the world. We hope that it makes you and puts a great impression on you, just like how it did on us while we made it. Enjoy!
Btw, we kind of messed up on the song, we didn't realize until it was too late. And we got carried away with Poverty, we didn't just take you to Poverty in Canada, we took you all around the world and taught you all different kinds of Poverty. Haha, but still.. enjoy! :)
Song:
Arms of An Angel - Sarah Mclachlan
Maeddah's and Hanbit's Multiplying Fractions


Question 9
BOB on Fractions
Adding Fractions
What I understand about it.. I understand that the rule for addition also appiles to subtraction. I also understand how to add fractions. Here, I'll show you :).
2/4+3/8
the first thing you have to do is look for the denominator that both 4 and 8 go into. Oh, make sure it's the smallest common denominator, so that you don't have to simplify it. The LCD is 4.
So,
2/4+3/8 < question
_/4+_/4 < the blank spots are the numbers we need to figure out.
So, you're probably wondering.. "how do we find those numbers?" This is what you do :). You take 4 and divide it by the denominator in the question. So, 4 divided by 4 is 1. You then multiply the answer you got with the numerator from the question. 1x2=2. So your first fraction is 2/4. To get the last fraction, you do the same thing. You take 4 and divide it by 8, which is 4. Then you multiply 4 with the numerator from the question, which is 12. Your second fraction is 12/4.
.. hmm.. so,
2/4+12/4 is your fraction
all you need to do now is add them together!
2+12=14
and the denominator stays the same because it's already.. the same.
14/4. < this is what you call an improper fraction! You need to fix it and make it into a mixed fraction. You have to find out how much times 14 goes into 4. _x4=a number close to 14? 3! 3x4=12. So 14 can only go into 4 1 time, and what do you have left over? 2. So your fraction would look like this..
12/4, BUT YOU STILL NEED TO SIMPLIFY! Reduce 2/4. 1/2.
FINAL ANSWER
11/2
Subtracting Fractions
For subtracting, you basically do the same thing.. but with the final result, you subtract. :) When you can subtract the fraction, you either need to borrow or turn them into improper fractions.
Problems..
My problems with fractions is that I don't really like them. I always have trouble with them! I got use to them this year though, and they were pretty easy and quick to learn. The only problem is I always mess up on my tests.
Scribe Post, March 10, 2009




The first square has an area of 1. It is an all perfect square because one is one square unit. The sidelines are 1, and you get this by square rooting the area (1). so, squareroot1 = 1. So, 1x1, and 1 squared. This square is also the smallest square out of all of them, and it also belongs in the perfect square club because the sideline numbers are perfect numbers and don't have decimals.
 This second square has an area of 2. It is NOT a perfect square because the square root of 2 is 1.414, which is obviously not a perfect number. So, the square cannot have a perfect sideline either. Squareroot2 = 1.414, 1.414x1.414 and 1.414 squared. This square is between the first and last square. This square would not be able to get into the perfect square club because the sidelines have decimals in them.
This second square has an area of 2. It is NOT a perfect square because the square root of 2 is 1.414, which is obviously not a perfect number. So, the square cannot have a perfect sideline either. Squareroot2 = 1.414, 1.414x1.414 and 1.414 squared. This square is between the first and last square. This square would not be able to get into the perfect square club because the sidelines have decimals in them. The third square has an area of 3. It is NOT a perfect square, because the square root of 3 is 1.732, which again is obviously not a perfect number. so the square cannot have a perfect sideline either. Squareroot3 = 1.732, 1.732x1.732, 1.732 squared. This square is between the first and last square. This square would not be able to get into the perfect square club because the sidelines have decimals in them.
The third square has an area of 3. It is NOT a perfect square, because the square root of 3 is 1.732, which again is obviously not a perfect number. so the square cannot have a perfect sideline either. Squareroot3 = 1.732, 1.732x1.732, 1.732 squared. This square is between the first and last square. This square would not be able to get into the perfect square club because the sidelines have decimals in them.Square 5 - The square has an area of 5. It is not a perfect square because the square root of 5 is 2.236, which is obviously not a perfect number. This square would not belong in the perfect square club because the sideline numbers are not full numbers. (decimals). Squareroot5 = 2.236, 2.236x2.236, 2.235 squared. You can also find the perimeter by adding all the sideline numbers together. 2.236+2.236+2.236+2.236=8.944.
Scribe Post for February 20
On February 20, we talked about the Pythagorean Theorem
Triangle

This is the triangle. The sides that make up the 90 degree angle are called legs and are labelled as A AND B. The hypotenuse is the C, and is the longest side of the triangle. You can always find it across from the 90 degree angle. Theta and Beta and the pictures show at the top corner and the bottom corner. The top one is the Theta and the bottom one is the Beta. Theta and Beta equal 90 degrees, which are called complementary angles.
 Square
SquareThis is a square, all the sides are equal. There are four 90 degree angles in this shape, which equals up to 360 degrees. (4x90=360) You can easily find the area or perimeter of the square if you know the measurement for one side. Example shown in the picture. One side is 5, so we know that all sides equal 5. 5x5, lxw, the area is 25. 5x5=25. Length-5, Width-5.
 Pythagorean Theorem
Pythagorean Theorem This is the the pythagorean theorem. The first square is 3x3, the second square is 4x4 and the last square is a combination of both squares, 5x5. You get to the last one, by putting the yellow square in the inside of the 5x5 square. It all fits in there, there is a little space left for the 3x3 square. So, you place it on there.
9+16=25
3x3+4x4=5x5
I hope this is what we learned! Sorry if it's not, the 873 one was the one scribe I could find. So, I'm going to pick someone who'll actually do it. Arielle. :) Love you too Arielle.
Help For Harbeck
All these pictures in the bottom are linked. How? The first, third and last picture are all connected to PYTHAGORAS, the second picture, because he was the one that created all of this. Pythagoras was the person that figured out the PYTHAGOREAN THEOREM. You can use the words "legs, hypotenuse, R.A.T, Greek, theorem" to help you with finding out and explaining your artifacts because each one connects to each picture. LEGS is connected with the Right Triangle. LEGS are the "A" and "B" on your Triangle, if you labelled it and "C" is the HYPOTENUSE (longest side of the Right Triangle). R.A.T is RIGHT ANGLE TRIANGLE, Greek is connected with Pythagoras because he is Greek, and also connects with the words THETA AND BETA. Theorem connects with every picture on this page, because it is the statement, theory of this all.



 The first shape is a RIGHT TRIANGLE. It is also known as R.A.T. (Right Angle Triangle). The right triangle has one 90 degree angle, which is on the corner. The first picture is the BETA, the second is the Theta. These angles both equal up to 90 degrees, which is called COMPLEMENTARY ANGLES. The longest line in the triangle is called the hypotenuse which is always labelled as C. The other two sides that make up the L, are called the legs which are always labelled as A or B.
The first shape is a RIGHT TRIANGLE. It is also known as R.A.T. (Right Angle Triangle). The right triangle has one 90 degree angle, which is on the corner. The first picture is the BETA, the second is the Theta. These angles both equal up to 90 degrees, which is called COMPLEMENTARY ANGLES. The longest line in the triangle is called the hypotenuse which is always labelled as C. The other two sides that make up the L, are called the legs which are always labelled as A or B.
 The second picture is PYTHOGORAS a Greek Genius. Many people call him FATHER OF MATH. He made the PYTHAGOREAN THEOREM, somethng I'll explain later. He discovered the circumference of the world, and figured out that the Sun goes around the Earth. He is a Vegan, someone who doesn't eat things that are alive and a teacher. He loves Music just like how he loves Math. He believed that he could make a square out of four right triangle angles and that he could make a triangle out of three squares. This is his proof. > He used the PYTHAGOREAN THEOREM and made these squares. One 3x3 square, one 4x4 square and one 5x5 square which was made from both 3 and 4 squares. The outside boxes are the 3x3 boxes and the inside boxes are 4x4.
The second picture is PYTHOGORAS a Greek Genius. Many people call him FATHER OF MATH. He made the PYTHAGOREAN THEOREM, somethng I'll explain later. He discovered the circumference of the world, and figured out that the Sun goes around the Earth. He is a Vegan, someone who doesn't eat things that are alive and a teacher. He loves Music just like how he loves Math. He believed that he could make a square out of four right triangle angles and that he could make a triangle out of three squares. This is his proof. > He used the PYTHAGOREAN THEOREM and made these squares. One 3x3 square, one 4x4 square and one 5x5 square which was made from both 3 and 4 squares. The outside boxes are the 3x3 boxes and the inside boxes are 4x4.
 The third picture is the PYTHAGOREAN THEOREM, I was talking about earlier. I think that this forumla is the relation to all three sides of the triangle. The first picture shows you how the pythagorean theorem works. I have a square of 3x3 and a square of 4x4. Harbeck gave us the assignment to put both squares together to make one square. The last square, 5x5 is the square that you should get when you put both squares together. The outside boxes are from the 3x3 square and the inside boxes are from the 4x4 square. The pythagorean theorem works for this, because 3x3 = 9, 4x4 = 16, and 5x5 = 25. 9+16=25. If you don't know the c2 side of a triangle (hypotenuse), then you find it by using what you know, and the pythagorean theorem. pretend one side of the triangle is 3 (side b) and one side of the triangle is 2 (a). the first thing you do is write out the pythagorean theorem. a2+b2=c2. then you write down what you know.You know that a is 2 squared and b is 3 squared. So you write it out. 3x3+2x2=c2. Simpify. 36+4=40. Then you find the square root of 40, which is 6.324. c2 is 6.324.
The third picture is the PYTHAGOREAN THEOREM, I was talking about earlier. I think that this forumla is the relation to all three sides of the triangle. The first picture shows you how the pythagorean theorem works. I have a square of 3x3 and a square of 4x4. Harbeck gave us the assignment to put both squares together to make one square. The last square, 5x5 is the square that you should get when you put both squares together. The outside boxes are from the 3x3 square and the inside boxes are from the 4x4 square. The pythagorean theorem works for this, because 3x3 = 9, 4x4 = 16, and 5x5 = 25. 9+16=25. If you don't know the c2 side of a triangle (hypotenuse), then you find it by using what you know, and the pythagorean theorem. pretend one side of the triangle is 3 (side b) and one side of the triangle is 2 (a). the first thing you do is write out the pythagorean theorem. a2+b2=c2. then you write down what you know.You know that a is 2 squared and b is 3 squared. So you write it out. 3x3+2x2=c2. Simpify. 36+4=40. Then you find the square root of 40, which is 6.324. c2 is 6.324.

The last picture is a square. It has 4 90 degree angles. All of the square equals up to 360 degrees. (90x4=360) You can make 2 right triangles out of this square by cutting it one of the corners. Like the first picture. The lines on the square tells you that all sides are equal, which means that this is a square and not a rectangle. If you know one side of the square, you know it all. You can find the area and perimeter. Pretend the square is 5 in length, it is also 5 in width. You can find the area by lxw, 5x5. The area is 25.
I care.. because I care. Education is important to everyone, I'm lucky to be attending a school without having to wait on the waiting list. I should appreciate it and do everything I can to successfully graduate it. (.. I don't know if I was actually suppose to answer this question or not.)
Math Video
I can't add this part to the PYTHAGOREAN THEOREM section because I have already published and made it into a wmv file. So, I'll just add the last part here.

I couldn't find our HOW TO FIND C video, so I'll just write about it, just to get a few marks atleast. Let's pretend you have a triangle. Side A is 4 and side B is 5. We need to find C, the hypotenuse. So, let's write out the question. a^2+b^2=c^2. Now we fill in what we know. We know that A is 4, so 4^2 and B is 5. So, 5^2. 4^2+5^2=c^2. 4x4+5x5=c^2. Now we simplify it. 16+25=41. To find out what c is, we need to also find the square root of 41. 6.403 is the square root, so that's the measurement for 41.
Pythagoras Homework

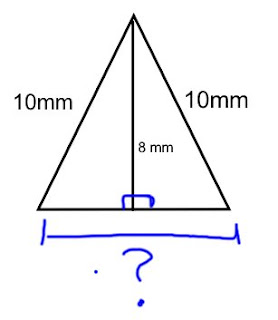 This is the Math Homework we received from Harbeck on February 23. We are suppose to find the base, which is why there is a question mark on there. The second picture shows how you solve c, just click on it to make it larger. I know what a is (8mm), so I can use that in my equation. I know what c is, (10mm), I can also use that in my equation.
This is the Math Homework we received from Harbeck on February 23. We are suppose to find the base, which is why there is a question mark on there. The second picture shows how you solve c, just click on it to make it larger. I know what a is (8mm), so I can use that in my equation. I know what c is, (10mm), I can also use that in my equation. The square is 225cm2. we find the square root, which is 15. Now we know that side b is 15, and side a is 15. since both are the same size. Now all we need to do is solve C using the Pythagorean Theorem. a2+b2=c2, 15x15+15x15=c2, 225+225=450. We need to find the square root of 450, which is 21.213. We now know that the Hypotenuse, which is always labelled as c is 21.213. we now try to find the perimeter. We multiply 21.213 by 4 or add 21.213 four times, because there are triangles in this picture, making 4 hypotenuse. 21.213x4=84.852. Then you multiply the legs which are labelled as a and b by 4 (or add 15 four times), because there are four triangles in this picture. 15x5=60. you then add them together. 60+84.852=144.852. the perimeter of this board is 144.852.
The square is 225cm2. we find the square root, which is 15. Now we know that side b is 15, and side a is 15. since both are the same size. Now all we need to do is solve C using the Pythagorean Theorem. a2+b2=c2, 15x15+15x15=c2, 225+225=450. We need to find the square root of 450, which is 21.213. We now know that the Hypotenuse, which is always labelled as c is 21.213. we now try to find the perimeter. We multiply 21.213 by 4 or add 21.213 four times, because there are triangles in this picture, making 4 hypotenuse. 21.213x4=84.852. Then you multiply the legs which are labelled as a and b by 4 (or add 15 four times), because there are four triangles in this picture. 15x5=60. you then add them together. 60+84.852=144.852. the perimeter of this board is 144.852.
Pay It Forward
For my act of kindness, I made cards with simple messages like "Thank you for having a caring heart and showing it towards many people.". In some cards, I also added "I may be a stranger, but I know that everyone has a pure heart. No matter if they show it, or if they keep it hidden behind their sour faces." I also added a piece of paper which had Psalm 139. My purpose for these cards is to make people smile. You may not think it's a big thing, but really.. smiles can make someone else's day. It can ever SAVE a life. A lot of people suffer from pain everyday. They either show it, or keep it inside of them. I hope that IF they ever read my cards, they would smile and understand that there are people out there that care for them.. even complete strangers. At the end of most of my cards, I added a simple "Thanks, it is greatly appreciated by a stranger. :) And "Anonymous" ". With my act of kindness, I think I helped different kinds of people. I'm not really sure WHO I helped, since my cards were anonymous.. but I'm guessing that I helped or gave a smile to different people. I placed 9 of these 29 cards on cars at the Chapters Parking Lot, so it would REALLY be anonymous. I still plan to place the rest of these cards in the mailboxes on my street and different streets.
The reason why I added the Bible verse: Psalm 139 was because that verse explained that everyone is loved, even if they do something that is not forgivable. There are many people out there that feel they are not loved, not cared for, and just plain are lonely. I'm hoping that one of those people got my cards and actually take the time to read them.. because it could change who they are as a person and their perspective of the world. I really do hope that I helped someone out that really needed it. I wanted to spread my religion as well as my kindness. I'm not sure if it was the right thing to do, considering the fact that not everyone is Christian. But I was/am always encouraged to spread it around me, so I did.


When I did my "act of kindness", I really felt excited and hopeful. I felt like staying beside those cars and houses, and wait for their owners to open the cars. I really hope that it made a lot of people smile. I'm hoping that "people I helped" actually opened the cards and read them. I hope they didn't throw it out.. and think that it's some kind of advertising paper. On the front part of the envelope, I wrote a simple "Pay it forward, do something NICE for someone ELSE."

I do think that one person makes a big difference. It's like a voting poll.. or voting for a new Class President, or something. You may not THINK that one simple vote from one person makes such a big difference.. but if the total of those votes are a tie, then it might have been better if you voted. You see, the world we live in needs a LOT of help. Especially the places that aren't so wealthy as.. us. They need every single person out there donating food, money, clothing for them to survive.
The Great Big Book of Algebra
Adding Integers Poem (A Diamante Poem)
Adding Integers
Adding
Free Verse: Subtracting
Subtracting!
When you sutbract,
you must attack the opposite like terms.
if you do not,
you will be caught,
in a big mess returned!
Multipication Rule "Ron's Rule" (Free Verse)
Ron's Rule
with something ridiculous like a positive number,
Free Verse: Partitive Division
Partitive Division
I thought really really really hard in my head.
Cinquain: Quotative Division
Quotative Division
Quotative
Negative, positive,
Script:
Apple - Hey Pear, how's it going?
Pear - Oh, hi Apple. Almost didn't see you there! Anyway, It's good It's good. I'm currently working on this math problem my sister gave me.. it kind of well, struck me. i'm pretty clueless right now!
Apple - Oh? Well, let's here the question! Maybe I can help.
Pear - n+3-5n+12. Think you can answer that? Look at those.. letters! I have no idea why their there..
Apple - Oh, those are variables! We use them in Alegbra to represent a number. Don't worry, Alegbra's easy. Now, tell me. What do you think the answer is?
Pear - Hm.. -6n+15.
Apple - Let's see if you're right. You group the same terms together.. which are n and 5n. And 3 and 12. Make sure you bring the operation signs with your numbers! Next we put them together.. hm, -5n+n+12+3. -5n+n=-4n, and 12+3=15! So the answer is -4n+15.
Pear -.. Oh. But I got -6n+15? Isn't that right?
Apple - Oh! No, no. Nice try there Pear, but you always, always have to look at the operation sign! Remember I told you take the operation signs with your numbers. I think you forgot the 5n was negative and added it.
Pear - Oh, thanks Apple!
Apple - Anytime, having anymore troubles?
Pear - .. I'm so sorry Apple to bother you! But I'm really not believing you when you say that Alegbra's easy. It's pretty hard to me!
Apple - Oh, don't worry about it Pear. You'll get it soon. I promise. Now, what's the next question?
Pear - 2+4(3n+8).
Apple - Oh! That's easy. For this question, we have to Distribute the Property. Here's what I mean.. well, wait. What do you think the answer is?
Pear - 12n+10.
Apple - Let's see if you're right! You first have to multiply the number that is touching the bracket with the closest number. So, for this question.. the multiplying number would be 4. And the first number TO multiply is 3n. 4x3n=12n. Then we multiply again, using 4.. but this time multiplying TO 8. So, 4x8=32. The next thing we do, so put the like terms together. 12n+32+2. The last step is to add the numbers that can... well, be added! so, 32+2=34. The answer is 12n+34.
Pear - Wow Apple, you're so smart! I think I'm starting to get it! I know why my answer was wrong! I forgot to multiply 4 with the number 8. I just added 8 and 2 together, which equalled 10. That's how I my answer, 12n+10. Whoops!
Apple - See, I told you Pear! Algebra's easy.. to everyone who tries.
(Changed some things in the movie to make script shorter)
Harbeck! I can't add Pear's mistake, my script is too long. So, I'll just
put Pear's mistake here.
Q:2 + 4(3n+8)
(4)8=32
2+32+12n
34+12n
Oh, and I know I spelled ALGEBRA wrong. I just can't fix it, because
I already published. That's what I get for publishing without rereading.
Here are some Additive, Subtractive, Multipicative and Divisive Equations!
RULES:
Isolate
Additive:

I solved this equation by drawing out the question. I drew one variable, which is the long green block, 3 constants, which are the red square blocks, and 5 constants which are the red square blocks after the equal sign. To isolate the variable, I added the opposite, which was -3 to +3. I was left with n. I added -3 to the answer (6). 3 postives and 3 negatives cancelled out each other and I was left with 2. N (variable) = 2 (constant). All I had to do was verify, which is just replacing the variable with the answer. On the other side, I did the same thing, but not using pictures. I isolated, cancelled the opposite, balanced and verified.
Subtractive:
 I solved this equation by drawing out the question. I drew one variable, which isthe long green blook, 4 negative constants, which are the red square blocks, and 7 constants which are the red square blocks after the equals sign. To isolate the variable, I added the opposite, which was +4 to -4. I was left with n. I added +4 to the answer 7, which gave me 10. N (variable) = 10 (constant). All I had to do was verify, which is just replacing the variable with the answer. On the other side, I did the same thing, but not using pictures. I isolated, cancelled the opposite, balanced and verified.
I solved this equation by drawing out the question. I drew one variable, which isthe long green blook, 4 negative constants, which are the red square blocks, and 7 constants which are the red square blocks after the equals sign. To isolate the variable, I added the opposite, which was +4 to -4. I was left with n. I added +4 to the answer 7, which gave me 10. N (variable) = 10 (constant). All I had to do was verify, which is just replacing the variable with the answer. On the other side, I did the same thing, but not using pictures. I isolated, cancelled the opposite, balanced and verified.
Multipicative: I solved this equation by drawing out the question. I drew two variables and 6 constants. The first thing I had to do was equally distribute the contants (6) with the 2 variable (2n). I drew the 1 variable, and put 3 constants beside it. I did the same with the remaining. I soon found out that one variable equals 3 positive contants. Then I circled each group. All I had to do was verify, which is just replacing the variable with the answer. On the other side, I did the same thing, but not using pictures. I isolated, cancelled the opposite, balanced and verified.
I solved this equation by drawing out the question. I drew two variables and 6 constants. The first thing I had to do was equally distribute the contants (6) with the 2 variable (2n). I drew the 1 variable, and put 3 constants beside it. I did the same with the remaining. I soon found out that one variable equals 3 positive contants. Then I circled each group. All I had to do was verify, which is just replacing the variable with the answer. On the other side, I did the same thing, but not using pictures. I isolated, cancelled the opposite, balanced and verified.
Divisive:
I solved this equation by drawing the question. I drew one variable, and wrote down the dividing sign and numbers. After I was finished, I took the number four and multipied it with 4 and the answer, 3. This is the way you isolate. Then I took 3 and four, which had a bracket touching.. which meant they are multipying. I multipied then together and got 12. N(variable) = 12(constant). All I had to do was verify, which is just replacing the variable with the answer. On the other side, I did the same thing, but not using pictures. I isolated, cancelled the opposite, balanced and verified.
Chapter 4: Algetile Video
During class, we were told to make a video about algebra equations using aletiles. We had to work on it at lunch, because we didn't get to finish it during class. So, sorry for the background noise! Props to: Tracy, Hanbit, and Maeddah.
Labels: algetile, greatbigbook, intpoetry, onestep, peachy841, xtranormal
Poetry Introduction - Scribe Post for December 1, 2008.
In Class or.. a summary for what Harbeck said on the math page.
- Ms. Hay told us that we have to make Integer poems, which is no surprise since Harbeck told us on Wednesday.
- 5 Integer poems. Pick any kind you want, (from the paper she gave us).
- Poem must be about the following: Adding Integers, Subtracting Integers, Partitive Division, Quotative Division , The "Rule for Multiplying" integers (Ron's Rule, Pratts Law, Mel's Rockpile etc)
- You need 3 different types of poetry in Chapter One. You can do the following : Haiku, Tanka, Cinquain, Free Verse Poetry, Picture, Diamante
- ALL DUE FRIDAY!
So, during class we started our poems. But it was SOO hard, especially if you're sitting beside the most annoying..ist? boy in the world.. : CASEY. Haha, just kidding. :) Here's one of my ROUGH COPIES. It's not a FOR SURE poem, just something I tried out.
Diamante: Diamante is the Italian word for diamond. The poetic form takes the shape of a diamond when it is completed. A diamante is a seven line poem.There are two patterns to choose from. Pattern one develops one topic. Pattern two starts out with one theme and in the middle begins to move toward an opposite theme.
PATTERN ONE:
Line 1: Choose a topic (noun)
Line 2: Use two describing words (adjectives)
Line 3: Use three action words (verbs)
Line 4: Use a four-word phrase capturing some feeling about the topic
Line 5: Use three action words (verbs)
Line 6: Use two describing words (adjectives)
Line 7: Use a synonym for an ending word (noun)
Example 1: This poem expresses one theme about a pop singing star.
Star
Famous, successful
Singing, dancing, shouting
Mesmerizing the adoring audience
Performing, working, reaching
Frenzied, dazzling
Showman
My Tryout.
Adding Integers Poem
Adding,
Problem Solving, simple
Thinking, increasing, gaining,
always trying your hardest,
receiving, completing, finishing,
Easy, fun to do,
Combining
Here are some sites that might help you guys write some poems!
Tanka:http://www.edu.pe.ca/stjean/playing%20with%20poetry/Hennessey/how_to_write_a_tanka_poem.htm
Haiku:http://www.edu.pe.ca/stjean/playing%20with20poetry/Hennessey/how_to_write_a_tanka_poem.htm
Cinquain:http://www.canteach.ca/elementary/poetry5.html
Free Verse:http://www.edu.pe.ca/stjean/playing%20with%20poetry/Hickey/Free%20Verse.htm
I can't find one about Picture Poems
Diamante: http://www.franklinlakes.k12.nj.us/famsweb/curriculum/English/diamantepoems/diamante.html
So, I guess that's it. That's all I got completed, well I mean.. this was the only 'rough copy' I had for my poems. I don't want the world to see MY REAL poems yet anyway! Haha, Good luck on your poems!
oh, and the next scribe is.. Tracy.
BTW, please comment and make corrections for me! Especially you Harbeck, if this wasn't how I was suppose to do the scribe for December 1, tell me! So I can fix it as soon as possible. Thanks. Oh, and I'm not really sure if there is a math/unit test tomorrow. But you guys should still study everything that we learned for this unit (Not Poetry)!
Bye, bye.
Maeddah's Integer Story
One morning, Aly Polish woke up. She brushed her teeth, showered, changed her clothes and ate breakfast. It was amazing how SLOW it took her to do these things. It was the same thing she did everyday, never changing her ways. Except this day was different.. there was a little box waiting outside her home door when she stepped outside. She picked up the box, curious of what was inside. Suddenly, a strange yellow flower came out.. and Aly Polish was pulled into a world full of choas. October 25, 2008 was the last day anyone has seen Aly Polish.
"Where am I?'' She thought, while realizing she wasn't at her house anymore. She was surrounded by letters, numbers, words, equations.. and that strange yellow flower that pulled her into this world. At first, she was afraid.. then angry. ''Why had this flower pulled me into this world?!'' she would constantly think. She tried to hold it in, but she couldn't. She needed to explode. She needed to yell at that dumb flower. So she picked it up, and yelled. She pulled all the pedals.. until the flower spoke.
''What is it you want? Are you wondering how to get out of this world? Would you like me to tell you how, or will you just keep pulling my pedals away until I rot?'' Aly.. suddenly forgetting her anger.. hurried to reply.
''Yes, yes yes!''
''Good child. The only way you can get away from me is by answering FOUR different integer questions. I will ask you one, but you must find the four other questions yourself.
''Now, answer this. Let's see how smart you really are. (+4)+(-7)=?''

''Hmm..'' Aly thought. ''I can solve this question by drawing out integer chips, and crossing out zero pairs!'' She quickly pulled a leaf from the palm trees and started working on her assignment.. while the strange flower started at her with a curious face.
'The answer's (-3)!'' Aly said excitedly. Happy that she would be able to go home.. at last.
''Good job child. You're smarter than I thought.'' The flower said, as it walked away. ''Now run along..''
''But, wait! How do I get home?! You said that if I answer your question, I could go home!'' Aly yelled desperately.
''Child, you need to clean your ears. I said that if you answered my question, I would leave you alone. So, here I am. Doing the thing I promised..'' The flower said. ''Goodbye!''
''How will I get home now?! I have to find the other 3.. special.. creatures ad answer their questions!'' Aly said as she run towards every little thing, trying to start a conversation with them. Too bad none of them responded back. Except for this little bumble bee, that was sleeping peacefully on a tree.
''Buzzzzz, zzzzZzZZzZzzzzZ.. honey..''
''Uhm, hello?! I know you're sleeping, but could you PLEASE HELP ME? I don't belong in this world filled with numbers, letters, questions.. I need to go home. I need to go home!'' Aly said to the buzzing bee.
''Huh?!'' The bee replied, slowly waking up. ''What is it?! You flithy human. What do you want? Can't you see I'm sleeping? It's been a while since I've had such a good dream! I will punish you! I WILL, I WILL!'' The bee said, nearly shouting.
''Wait! Please no! Please let me go, please don't harm me! I'll do anything! Perhaps an integer question? If I don't get it right, you can punish me all you want! But if I get it right, you let me free. Besides, I'm not too good at those questions..'' Aly said, hoping her little lie would trick the bee.
''Quite excellent.. if you lose, I will make you put your hand into my clan's enemy's hive! I will make you steal all their honey, while they sting your poor human hand!'' The bee said excitedly.

''Alright, lets start with the question. (-6)+(-3)=?'' Again, Aly grabbed leaves and started on her math question. but this time using a number line.
''The answer is (-9)!''
''Why! That's right! Gr, I have a feeling you tricked me. Lucky YOU! I'm leaving.'' And so, he left. Aly Polish kept on walking, feeling confident of what she had just done. She kept walking, and walking.. until she reached a cave, with a little note says..
''Those who want to pass, will have to answer this integer question. (-7)+(+6)=?''
 ''Wow, this world and their integer questions! Guess I have to start..'' Once again, Aly grabbed a leaf and started her question. This time she used the 'HAVE AND OWE' method.
''Wow, this world and their integer questions! Guess I have to start..'' Once again, Aly grabbed a leaf and started her question. This time she used the 'HAVE AND OWE' method. And the doors of the cave opened. Aly walked on inside, not surprised by the many letters and numbers inside. She walked and walked until she reached a dead end. She desperately looked around, trying to find a way out. But everything was closed. The door in the front was closed once again. The only thing he could see besides the letters and numbers was this sheet of paper. With one sentence, (-5)+(+5)=?. Aly, sighing.. started to write on the sheet on paper. Using no method at all. For this question was a no brainer. After finishing the question, Aly waited a while. But nothing happened!
And the doors of the cave opened. Aly walked on inside, not surprised by the many letters and numbers inside. She walked and walked until she reached a dead end. She desperately looked around, trying to find a way out. But everything was closed. The door in the front was closed once again. The only thing he could see besides the letters and numbers was this sheet of paper. With one sentence, (-5)+(+5)=?. Aly, sighing.. started to write on the sheet on paper. Using no method at all. For this question was a no brainer. After finishing the question, Aly waited a while. But nothing happened!  ''The answer is (+7)!'' Aly said.
''The answer is (+7)!'' Aly said. ''Hello, a little pixie on the other side of the cave told me these instructions. He said that one of you guys could take me home. Maybe you could?'' Aly asked, in the kindest way she could.

The End.
October 14, 2008 - Probability
HERE WE GO. (oh, and were suppose to pick 3 questions from each section of the page)
Questions 1-14, Single Event Probability (One thing happening)
4. You roll a number cube numbered from 1 to 6.
P(not a 6)
Express the probability as a fraction, and turn it unto a percentage.
7. A jar contains 24 black, 11 orange, 10 brown, and 9 violet marbles. A marble is drawn at random.
P(violet)
Express the probability as a fraction.
8. A number from 9 to 20 is drawn at random.
P(a number divisible by 2)
Express the probability as a percent. Round to the neaest percent.
Questions 1-10, Multiple Event Probability (More than one thing happening)
1. You roll a number cube numbered from 1 to 6
You then spin a spinner with 3 sections each with a different color. The spinner has the colors orange, gray, and pink.
P(2, 4, 1, 5, or 3 and orange)
* (AND is very important, it tells you that there are more things happening)
btw, im sorry that its really messy! ^
2. You flip a coin and toss a 1-6 number cube.
P(5 and tails)
5. You flip a coin and toss a 1-6 number cube.
p(not tails and not a 3)

YAY, im done! :) look at all that hard work. hahaha!
uhm, the next scribe person is.. DUN DUN DUN.. ARIELLE!













