So, in this scribe I will be talking about the first four questions from the quiz.


Just so you know, if I put something in RED that means that I'm answering it, or that it is the question. If something is in GREEN then that would be the answer to the question.
Number 1 :
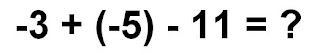
I don't know what you did, but instead of subtracting the 11, I added a negative 11.
The question then looked like this :

To solve this question, I split this question into two parts.
The first thing I did was add the negative 3 with the negative 5 which equaled negative 8.
-3 + (-5) = -8
Next I added the negative 8 with the negative 11 which then equaled negative 19.
-8 + (-11) = -19
Number 2 :
Number 2 is not as easy as number 1, but if you had trouble doing this, I will explain how I figured it out.

The first thing I did, was answer whichever pairs I can. So I decided to multiply the 5 and negative 4, and the negative 2 and negative 1.
(5)(-4) + (-2)(-1)(-6) = ?
(-20) + (2) (-6) = ?
To solve the first one, I just remembered the saying that we do when we multiply (look at your barn doors project). '5 groups of negative 4'. You should then know that the answer is negative 20. For the second part that I did, I said the other saying for negative integers at the front. 'Remove 2 groups of negative 1'. And if you did your multiplication homework, you then should know that the answer is negative 2. Anyways, time to finish the equation.
(-20) + (2)(-6) = ?
Two groups of negative six equals ?..
(-20) + (-12) = ? / Negative 12!
Now finish off the question by adding the remaining integers.
(-20) + (-12) = (-32)
Number 3 :
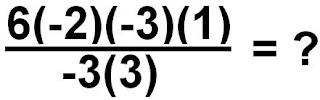
Number 3 is way harder than the previous questions since it includes dividing. Before we divide we must come up with one integer on the top and one integer on the bottom. Once again, I just divided the question in parts to make it easier.
6(-2) (-3)(1)
───────── = ?
-3(3)
To solve this, just use the "rule for multiplying" when you try to figure out a multiplication question. If you did it correctly, your answers should look something like this :(-12) (-3)
─────── = ?
(-9)
Now answer the top part of the fraction/division sign.
'Remove 12 groups of negative 3'. What does that give you?
(-36)
──── = ?
(-9)
What would that question be; quotative, partitive, or multiplicative inverse?
If you guessed quotative, then you're right!
'How many negative nines are in negative 36'?
(-36)
──── = 4
(-9)
Number 4 :

This question I will have to make fairly quick because it's getting late.
(14) + (-6)
──────── = ?
(-4)
Next add the two integers on the top.
(8)
── = ?
(-4)
What would that question be; quotative, partitive, or multiplicative inverse?
If you guessed multiplicative inverse then you're right!
'N x (-4) = (8)'. What is N?
(8)
── = (-2)
(-4)
________________________________________
Anyways, I'm done my scribe. Sorry for it being done so late but I had many distractions along the way. One of them including a nose bleed which really bothered me. So yeah, anyways the next scribe is ... ADRIAN R.! Have fun and good luck.
Oh yeah, please comment and tell me my mistakes so I can make my next scribe better. Thanks in advance!
Oh yeah, please comment and tell me my mistakes so I can make my next scribe better. Thanks in advance!




 Today in math class we did the rest of page 6 in our green booklets
Today in math class we did the rest of page 6 in our green booklets 



 .
. 
